"מיצ'יו קאקו הוא מספר סיפורים מחונן, המפיח חיים בנתונים יבשים ובתיאוריות מסועפות ומנגיש אותם לקורא הסקרן בצורה מענגת." וול סטריט […]
מבוא לתיאוריה הסופית
היא היתה אמורה להיות התיאוריה הסופית — מסגרת אחת ויחידה שתאחד את כל כוחות הקוסמוס ותכתיב את הכוריאוגרפיה של כל הדברים, מתנועת היקום המתפשט ועד למחול הזערורי ביותר של החלקיקים התת־אטומיים. האתגר היה כתיבת משוואה שהאלגנטיות המתמטית שלה תחבוק את כל הפיזיקה.
אחדים מהפיזיקאים הגדולים ביותר בעולם התמודדו עם האתגר הזה. סטיבן הוקינג אפילו נשא הרצאה שכותרתה ״האם קרֵב קץ הפיזיקה התיאורטית?״1
אם תתגלה תיאוריה שכזו כמוצלחת, היא תהיה גולת הכותרת של ההישג המדעי. זוהי משאת נפשם של הפיזיקאים, נוסחה אחת ויחידה שממנה יהיה אפשר, עקרונית, לגזור את כל שאר המשוואות, החל במפץ הגדול והלאה ממנו עד קץ היקום. היא תהיה המוצר הסופי של אלפיים שנות חקירה מדעית, מאז העלו הקדמונים לראשונה את השאלה, ״ממה עשוי העולם?״
זהו חזון עוצר נשימה.
חלומו של איינשטיין
בפעם הראשונה שנתקלתי באתגר שמציב החלום הזה, הייתי בן שמונה שנים. יום אחד בישרו העיתונים על מותו של מדען דגול. בעיתון היתה תמונה בלתי־נשכחת.
זה היה תצלום של שולחן הכתיבה שלו, ועליו פנקס פתוח. הכיתוב מתחת הכריז שגדול המדענים של זמננו לא הספיק להשלים את העבודה שבה התחיל. זה קסם לי. מה יכול להיות כל כך קשה, שאפילו איינשטיין הדגול לא יכול לפתור אותו?
הפנקס ההוא הכיל את התיאוריה של הכול הלא־גמורה של איינשטיין, שנקראה בפיו תיאוריית השדה המאוחדת. הוא ביקש משוואה שכל אורכה אולי לא יעלה על זרת אחת, משוואה שתאפשר לו ״לרדת לסוף דעתו של אלוהים״, כפי שהוא ניסח זאת.
כיוון שלא הערכתי נכונה את ממדי הבעיה הזאת, החלטתי ללכת בעקבות האיש הדגול ההוא, וקיוויתי למלא תפקיד פעוט בהשלמת החיפושים.
אבל רבים אחרים ניסו גם הם, ונכשלו.2 כפי שאמר פרימן דַייסוֹן, פיזיקאי מפרינסטון, הדרך לתיאוריית השדה המאוחדת סוגה בגוויותיהם של ניסיונות שנכשלו.
אבל כיום מאמינים פיזיקאים בכירים רבים שהם מתקרבים סוף־סוף לפתרון.
המועמדת המובילה (ולדעתי, היחידה) לתפקיד תיאוריית השדה המאוחדת נקראת תורת המיתרים, היוצאת מתוך ההנחה שהיקום עשוי לא מחלקיקים נקודתיים אלא ממיתרים רוטטים זעירים, כך שכל צליל מתאים לחלקיק תת־אטומי מסוים.
אילו היה לנו מיקרוסקופּ חזק די הצורך, היינו רואים שאלקטרונים, קווארקים, נייטרינים וכיו״ב אינם אלא רטיטות של לולאות זערוריות, דומות לגומיות. אם נפרוט על הגומייה מספיק פעמים ובדרכים שונות, ניצור בסופו של דבר את כל החלקיקים התת־אטומיים הידועים ביקום. המשמעות היא שנוכל לצמצם את כל חוקי הפיזיקה להרמוניות של המיתרים הללו. הכימיה היא הנעימוֹת שאפשר לנגן בהם. היקום הוא סימפוניה. וחשיבתו של אלוהים, שאיינשטיין כתב עליה באורח כה נמלץ, היא מוזיקה קוסמית שמהדהדת בכל המרחב־זמן.
אין זו שאלה אקדמית גרידא. כל אימת שהמדענים חשפו כוח חדש, הוא הטה את מהלך הציוויליזציה ושינה את גורל האנושות. לדוגמה, גילוי חוקי התנועה והכבידה על ידי ניוטון הניח את יסודותיהם של עידן המכונות והמהפכה התעשייתית. הסברי החשמל והמגנטיות על ידי מייקל פָרָדֵיי וג'יימס קלַרק מַקסוֶול סללו את הדרך להארת ערינו ונתנו לנו מנועים חשמליים ומחוללים, ובהמשך, תקשורת־בזק באמצעות רדיו וטלוויזיה. משוואת איינשטיין, E = mc2, הסבירה את מקור הכוח של הכוכבים וסייעה בחשיפת הכוח הגרעיני. וכאשר פענחו ארווין שרֵדִינגֶר, ורנר הַייזֶנבֶּרג ואחרים את סודותיה של תורת הקוונטים, הם העניקו לנו את מהפכת ההיי־טק של ימינו, עם מחשבי־על, לייזרים, האינטרנט וכל החפיצים המופלאים שמקיפים אותנו.
ביסודו של דבר, כל פלאי הטכנולוגיה המודרנית נולדו מעבודתם של המדענים שגילו בהדרגה את כוחות היסוד של העולם. כיום, ייתכן שהמדענים מתקרבים לתיאוריה שתאחד את ארבעת כוחות הטבע הללו — הכבידה, הכוח האלקטרומגנטי ושני הכוחות הגרעיניים, החזק והחלש. בסופו של דבר, אפשר שהיא תספק תשובות לאחדות מהתעלומות העמוקות ביותר והשאלות החשובות ביותר של המדע בכללותו, כגון:
• מה קרה לפני המפץ הגדול? ומדוע הוא התפוצץ בכלל?
• מה נמצא בצידו השני של חור שחור?
• האם מסע בזמן אפשרי בכלל?
• האם יש חורי תולעת שמוליכים ליקומים אחרים?
• האם יש ממדים גבוהים?
• האם יש רב־יקום של יקומים מקבילים?
ספר זה מתאר את החיפושים אחר התיאוריה העילאית הזאת, ואת כל העיקולים והתפניות המשונים בפרק זה בתולדות הפיזיקה, שהוא בלי ספק אחד המוזרים מכול. נסקור בו את כל המהפכות הקודמות, אלה שהעניקו לנו את פלאי הטכנולוגיה, החל במהפכה הניוטונית, עבור בהשתלטות על הכוח האלקטרומגנטי, המשך בפיתוח תורת היחסות והתיאוריה הקוונטית, ועד לתורת המיתרים של ימינו. לבסוף נסביר כיצד עשויה התיאוריה הזאת גם לחשוף את התעלומות העמוקות ביותר של המרחב והזמן.
צבא של מבקרים
אבל יש עדיין מכשולים בדרך. למול כל ההתרגשות שעוררה תורת המיתרים, מבקריה חשו להצביע על ליקוייה. ואחרי כל הפרסום וההתלהבות, ההתקדמות הממשית נבלמה.
הבעיה הבולטת ביותר היא שלמרות המחמאות בעיתונות ששיבחו את יופיָה של התיאוריה ואת מורכבותה, אין לנו שום ראיות מוצקות שאפשר להעמידן למבחן. בעבר התעוררה התקווה שהמאיץ הגדול להתנגשויות הַדרוֹנים (LHC) ליד ז'נבה — מאיץ החלקיקים הגדול ביותר בהיסטוריה — ימצא ראיות מוחשיות לתיאוריה הסופית, אבל אלה נותרו חמקמקות. LHC הצליח למצוא את בּוֹזוֹן הִיגס (המכוּנה ״חלקיק האלוהים״), אבל החלקיק הזה היה רק חלק קטן מכל מה שדרוש לתיאוריה הסופית.
אמנם הועלו הצעות שאפתניות לבנות יורשים ל-LHC, חזקים עוד יותר ממנו, אבל אין שום ערובה שהמכונות היקרות־מאוד הללו ימצאו משהו בכלל. איש אינו יודע לבטח באיזו אנרגיה נוכל למצוא חלקיקים תת־אטומיים חדשים שיוכלו לאמת את התיאוריה.
אבל ייתכן שהביקורת החשובה ביותר על התיאוריה היא שהיא מנבאת ריבוי יקומים. איינשטיין אמר ששאלת המפתח היא זו: האם היתה לאלוהים ברירה כשברא את היקום? האם היקום הוא ייחודי? תורת המיתרים היא ייחודית כשלעצמה, אבל נראה שיש לה מספר אינסופי של פתרונות. הפיזיקאים קוראים לזאת בעיית הנוף — העובדה שהיקום שלנו הוא אולי רק פתרון אחד בתוך אוקיינוס של פתרונות אחרים, תקפים כולם באותה המידה. אם יקומנו הוא אחת מבין אפשרויות רבות, איזו מהן היא שלנו? מדוע אנו חיים ביקום המסוים הזה ולא באחר? ואם כך, מהו כוח הניבוי של תורת המיתרים? האם היא תיאוריה של הכול, או רק תיאוריה של מה שלא יהיה?
אודה ואתוודה, יש לי חלק משלי בחיפושים הללו. אני עובד על תורת המיתרים מאז 1968, מאז הופעתה במקרה, בלי התרעה מוקדמת, ובלי שאיש ציפה לה. הייתי עד להתפתחותה המרשימה של התיאוריה, שהפכה ממשוואה יחידה לתחום מדעי עם מאמרי מחקר שיכולים למלא ספרייה. כיום, תורת המיתרים היא הבסיס לחלק ניכר מהמחקר שמתנהל במעבדות המובילות בעולם. אני תקווה שספר זה יציג בפניכם ניתוח מאוזן ואובייקטיבי של פריצות הדרך שהשיגה תורת המיתרים ושל מגבלותיה.
הוא גם יסביר מדוע החיפושים הללו שבו את דמיונם של בכירי המדענים בעולם, ומדוע התיאוריה הזאת הולידה יצרים כה עזים ומחלוקות כה חריפות.
1
איחוד — החלום הישן־נושן
כשאנו נושאים את עינינו אל הזוהר המפואר של שמי הלילה, כשאנו מוקפים בכל כוכבי הרקיע המזהירים, קל לנו להרגיש שהתפארת עוצרת הנשימה הזאת מציפה כליל את חושינו. דאגות היומיום שלנו מתחלפות באחדות מהשאלות המסתוריות ביותר שנשאלו אי־פעם.
האם יש תוכנית אב ליקום?
איך נוכל להבין קוסמוס שהוא בלתי־מובן למראית עין?
האם יש סיבה ותכלית לקיומנו, או שמא הכול חסר טעם?
אני נזכר בשיר מאת סטיבן קרֵיין:
אמר אדם ליקום:
״אדוני, אני קיים!״
״אבל,״ ענה לו היקום,
״עובדה זו אינה מעוררת בי תחושת מחויבות.״
היוונים היו בין הראשונים שניסו ברצינות להשליט סדר באנדרלמוסיה של העולם הסובב אותנו. פילוסופים כמו אריסטו האמינו שאת כל כולו אפשר לצמצם לתערובת של ארבעה מרכיבי יסוד: אדמה, אוויר, אש ומים. אבל כיצד יכולים ארבעת היסודות הללו ליצור את מורכבותו העשירה של העולם?
היוונים הציעו שתי תשובות, לפחות, לשאלה זו. את הראשונה נתן הפילוסוף דֶמוֹקרִיטוֹס, עוד לפני אריסטו. הוא האמין שאפשר לצמצם את הכול לחלקיקים זעירים, בלתי־נראים ובלתי־ניתנים להשמדה, שנקראו בפיו אטומים (לפי מילה יוונית שפירושה ״בלתי־ניתן לחיתוך״). אולם מבקריו ציינו שאי־אפשר להשיג ראיות ישירות לקיומם של אטומים, מפני שהם קטנים מכדי שיוכלו להיראות לעין. למרות זאת, היה ביכולתו של דמוקריטוס להציג ראיות עקיפות אך משכנעות.
ראו לדוגמה טבעת זהב. במרוצת השנים, הטבעת מתחילה להישחק. היא מאבדת משהו. מדי יום ביומו, כמה חתיכות זערוריות של חומר נושרות מעל הטבעת. לפיכך, גם אם האטומים בלתי־נראים, אפשר למדוד את קיומם בעקיפין.
גם בימינו אלה, רוב ההתקדמות המדעית שלנו מושגת בדרכי עקיפין. אנחנו יודעים ממה עשויה השמש, מהו המבנה המפורט של הדנ״א ומהו גיל היקום, הודות למדידות מעין אלה. אנחנו יודעים את כל זאת אף על פי שמעולם לא ביקרנו בכוכבים, לא נכנסנו לתוך מולקולת דנ״א וגם לא חזינו במו עינינו במפץ הגדול. הבחנה זו בין ראיות ישירות ועקיפות תתגלה כחיונית כשנגיע לדיון בניסיונות להוכיח תיאוריית שדה קוונטית.
חלוץ הגישה היוונית השנייה היה המתמטיקאי הדגול פִּיתָגוֹרָס.
התובנה הגדולה של פיתגורס היתה יישומם של תיאורים מתמטיים לתופעות ארציות, למשל מוזיקה. האגדה מספרת שהוא הבחין בדמיון בין הצלילים שמשמיעה פריטה על מיתרי לירה (נֵבֶל) לבין ההדהודים שעולים מחבטות פטיש במוט מתכת. הוא מצא שאלה כמו אלה יוצרים תדירויות מוזיקליות שרוטטות ביחסים מתמטיים מסוימים. כלומר, מקור המוזיקה הערבה כל כך לאוזן מצוי במתמטיקה של תהודות. דבר זה, חשב פיתגורס, אולי מראה שכל העצמים המרובים והשונים שאנו רואים סביבנו חייבים לציית לאותם חוקים מתמטיים.
הנה כי כן, לפחות שתי תיאוריות גורפות של עולמנו באו מיוון העתיקה: הרעיון שכל הדברים עשויים מאטומים בלתי־נראים ובלתי־ניתנים להשמדה, ושאפשר לתאר את רבגוניות הטבע באמצעות המתמטיקה של הרטיטות.
למרבה הצער, עם קריסתה של הציוויליזציה הקלסית, אבדו הוויכוחים והדיונים הפילוסופיים הללו. הרעיון שלפיו תיתכן פרדיגמה שמסבירה את היקום נשכח לאלף שנים כמעט. אפלה ירדה על העולם המערבי, ואת מקום החקירה המדעית תפסו כמעט כליל אמונות תפלות, כשפים ואמונה בנסתר.
הרנסנס: לידה מחדש
במאה השבע־עשרה קמו כמה מדענים דגולים, קראו תיגר על הסדר הקיים והחלו לחקור את טבע היקום, אלא שהם נתקלו בהתנגדות עזה ונרדפו עד חורמה. יוהנס קֶפּלֶר, אחד הראשונים שיישמו מתמטיקה לתנועות כוכבי הלכת, היה יועץ לקיסר רודולף השני, וייתכן שהוא ניצל מרדיפה בכך שהכניס באדיקות רכיבים דתיים לעבודתו המדעית.
גורלו של הנזיר־לשעבר ג'ורדנו בּרוּנוֹ לא שפר עליו במידה שכזו. בשנת 1600 הוא הועמד למשפט האינקוויזיציה ונידון למוות על כפירה. הוא הוצעד ברחובות רומא, עירום ועריה ובפה חסום, ולבסוף נשרף חיים על המוקד. ומה היה פשעו? בראש ובראשונה, הוא הכריז שייתכנו חיים בכוכבי לכת שסובבים כוכבים אחרים.
גלילאו הגדול, אבי המדע הניסויי, היה רחוק כחוט השערה מגורל דומה. אך שלא כמו ברונו, גלילאו חזר בו מהתיאורייות שלו כאשר איימו עליו חוקריו במוות. למרות זאת, הוא הותיר מורשת נצחית באמצעות הטלסקופּ שלו — אולי ההמצאה המהפכנית והחתרנית ביותר בכל תולדות המדע. הודות לטלסקופּ היה אפשר לראות בפועל ממש שהירח מנוקד במכתשים; שלנוגה יש מופעים שמעידים כי הוא חג סביב השמש; ושלכוכב הלכת צדק יש ירחים. כל אלה היו רעיונות כפירה.
למרבה העצב, הוא הושם במאסר בית, איש לא הורשה לבקרו, ולבסוף הוא התעוור. (אומרים שהסיבה היא שהוא הביט פעם בשמש דרך הטלסקופּ.) גלילאו היה שבור ורצוץ במותו, אבל ממש באותה שנה נולד באנגליה תינוק שהיה עתיד, בהתבגרו, להשלים את התיאוריות הלא־גמורות של גלילאו ושל קפלר, ולתת לנו תיאוריה מאוחדת של הרקיע.
תיאוריית הכוחות של ניוטון
אייזיק ניוּטוֹן היה אולי גדול המדענים שחיו אי־פעם. בעולם של כשפים ואמונות תפלות, הוא הרהיב עוז, העלה על הכתב את החוקים האוניברסליים של הרקיע והשתמש במתמטיקה חדשה שהמציא, הקרויה חשבון אינפיניטסימלי, לחקירת הכוחות. כפי שכתב הפיזיקאי סטיבן וַיינבֶּרג, ״באייזיק ניוטון מתחיל למעשה החלום המודרני על תיאוריה סופית.״3 בשעתו, התיאוריה שלו נחשבה לתיאוריה של הכול — כלומר תיאוריה שמתארת את כל התנועות.
הכול החל כשהוא היה בן עשרים ושתיים. אוניברסיטת קיימברידג' סגרה את שעריה בגלל המוות השחור, והוא נאלץ להפסיק את לימודיו בה. יום אחד ב-1666, בעת שטייל באחוזה הכפרית של סבו, הוא ראה תפוח נופל, ומיד שאל את עצמו שאלה שהיתה עתידה לשנות את מהלך ההיסטוריה האנושית.
אם תפוח נופל, מדוע אין הירח נופל גם כן?
לפני ניוטון הורתה הכנסייה שיש שני סוגי חוקים. הסוג האחד מקיף את החוקים שחלים על כדור הארץ, מקום שנשחת בגלל חטאיהם של בני התמותה. הסוג השני הוא החוקים הטהורים, המושלמים וההרמוניים של הרקיע.
עיקר רעיונו של ניוטון היה הצעתה של תיאוריה מאוחדת, שחלה על הרקיע כשם שהיא חלה על כדור הארץ.
הוא שרטט בפנקסו תמונה הרת גורל (ראו איור 1).
אם יורים כדור תותח מראש הר, הוא עובר מרחק מסוים עד שלבסוף הוא פוגע בקרקע. אבל אם יורים את הכדור במהירויות יותר ויותר גבוהות, הוא נע יותר ויותר רחוק לפני שובו לקרקע. בסופו של דבר, הוא משלים הקפה מעגלית סביב כדור הארץ וחוזר ופוגע בראש ההר. מסקנתו של ניוטון היתה שחוק הטבע המושל בתפוחים ובכדורי תותח — חוק הכבידה — גם מחזיק את הירח במסלולו סביב כדור הארץ. הפיזיקה הארצית והשמֵימית, אחת היא.
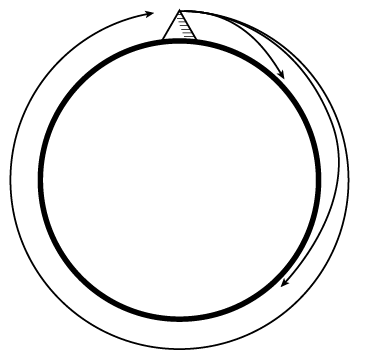
איור 1. אפשר לירות כדור תותח באנרגיות יותר ויותר גבוהות, כך שלבסוף הוא מקיף את כל כדור הארץ וחוזר לנקודת המוצא שלו. ניוטון אמר שהדבר מסביר את מסלול הירח, ובכך איחד את החוקים הפיזיקליים החלים עלי אדמות עם החוקים המושלים בגרמי השמים.
ניוטון הגיע למסקנה זו בכך שהציג את מושג הכוחות. עצמים נעים מפני שמושכים או דוחפים אותם כוחות שהם אוניברסליים ואפשר למדוד אותם בדייקנות בשיטות מתמטיות. (קודם לכן חשבו כמה תיאולוגים שעצמים נעים מפני שיש בהם ״שאיפות״, ולכן עצמים נופלים ארצה בגלל תשוקתם להתאחד עם האדמה.)
אבל ניוטון היה ידוע לשמצה כאדם מסוגר, והוא שמר חלק ניכר מעבודתו בסוד. לא היו לו ידידים, הוא לא היה מסוגל לנהל שיחת חולין, ולעיתים תכופות נכנס לקרבות עם מדענים אחרים על זכות הראשונים לתגליותיו.
ב-1682 התרחש אירוע סנסציוני ששינה את מהלך ההיסטוריה. שביט מפואר הופיע בשמי לונדון. החדשות היו שיחת היום בפי הכול בכול, ממלכים ומלכות עד קבצנים. מנין הוא בא? להיכן הוא הולך? מה הוא מבשר?
אחד מאלה שהתעניינו בשביט זה היה האסטרונום אדמוֹנד הָאלִי. הוא עלה לרגל לקיימברידג' כדי להתראות פנים עם אייזיק ניוטון המהולל, שכבר נודע לשם בזכות תיאוריית האור שלו. (ניוטון העביר קרן אור שמש דרך מנסרת זכוכית והראה כי האור הלבן מתפצל לכל צבעי הקשת. כך הוא הוכיח שאור לבן הוא למעשה צבע מרוכב. הוא גם המציא סוג חדש של טלסקופּ, שמשתמש במראות קעורות במקום עדשות.) כששאל האלי את ניוטון על השביט שהיה שיחת היום, הוא נדהם לשמוע שניוטון יכול להראות כי שביטים נעים במסלולים אליפטיים סביב השמש, ויש ביכולתו אפילו לנבא את מסלוליהם באמצעות תיאוריית הכבידה שלו. למעשה, ניוטון התחקה אחר השביט בטלסקופּ שהמציא, והוא נע בדיוק כפי שהוא ניבא.
האלי היה המום.
הוא הבין מיד שהוא ניצב בפני ציון דרך בתולדות המדע, והתנדב לשלם את הוצאות ההדפסה של הספר שנועד להיות אחת מיצירות המופת הגדולות של המדע, Philosophiæ Naturalis Principia Mathematica (העקרונות המדעיים של חוכמת הטבע), שידוע בקיצור בשם פּרִינקִיפּיָה.
יתר על כן, משהבין האלי כי חוקי ניוטון מנבאים ששביטים עשויים לחזור במרווחי זמן קבועים, הוא חישב ומצא שהשביט של 1682 עתיד לשוב ב-1758. (שביט האלי אכן חצה את שמי אירופה ב-25 בדצמבר 1758, כצפוי, והדבר סייע להנצחת שמותיהם של ניוטון והאלי, שכבר היו במתים שניהם.)
תיאוריית התנועה והכבידה של ניוטון ניצבת כאחד ההישגים הגדולים ביותר של רוח האדם, כעיקרון יחיד המאחד את חוקי התנועה הידועים. המשורר אלכסנדר פּוֹפּ כתב:
הטבע וחוקיו היו שרויים בחשכת שחור:
ויאמר אלוהים, יהי ניוטון!
ויהי אור.
אפילו כיום, חוקי ניוטון הם המאפשרים למהנדסי נאס״א להנחות את גשושות החלל שלהם ברחבי מערכת השמש.
מהי סימטריה?
חוק הכבידה של ניוטון ראוי לציון גם מפני שהוא מחונן בסימטריה, כך שהמשוואה נשארת זהה אם אנו מבצעים סיבוב. תארו לעצמכם ספֵירה שמקיפה את כדור הארץ. כוח הכבידה יהיה זהה בכל נקודה על פניה. למעשה, זו הסיבה לכך שיש לכדור הארץ צורה כדורית, ולא כל צורה אחרת: הכבידה דוחסת את החומר של כדור הארץ באופן אחיד. מסיבה זו, לעולם לא נראה כוכבים קובייתיים או כוכבי לכת פירמידליים. (לאסטרואידים קטנים יש בדרך כלל צורה לא סדירה, מפני שכוח הכבידה של אסטרואיד אינו מספיק חזק כנדרש לדחיסה אחידה שלו.)
מושג הסימטריה הוא פשוט, אלגנטי ואינטואיטיבי. זאת ועוד, לכל אורכו של ספר זה נראה שהסימטריה אינה סתם קישוט, תוספת נופך לתיאוריה, אלא היא למעשה סממן חיוני המלמד על איזה עיקרון פיזיקלי עמוק של היקום, המונח ביסוד הדברים.
אבל מה אנו מתכוונים להגיד, כשאנו אומרים על משוואה שהיא סימטרית?
עצם הוא סימטרי אם, אחרי שסידרנו את חלקיו מחדש, הוא נשאר בעינו — בלתי־משתנה. לדוגמה, ספֵירה היא סימטרית מפני שהיא נשארת בעינה אחרי שסובבנו אותה. אבל איך אפשר לבטא זאת בדרך מתמטית?
ראו את כדור הארץ המסתובב סביב השמש (איור 2). רדיוס מסלולו של כדור הארץ מבוטא על ידי R, שנשאר בעינו עם תנועת כדור הארץ במסלולו (בפועל, מסלול כדור הארץ הוא אליפטי, כך ש-R משתנה במקצת, אבל אין לכך חשיבות לצורך הדוגמה הנוכחית). הקואורדינטות של נקודה במסלול כדור הארץ נתונות לפי x ו-y. כשכדור הארץ נע במסלולו, x ו-y משתנים ברציפות, אבל R נשאר בעינו; המתמטיקאים אומרים שהוא אִינוַוריָאנטִי (בלתי־משתנה).
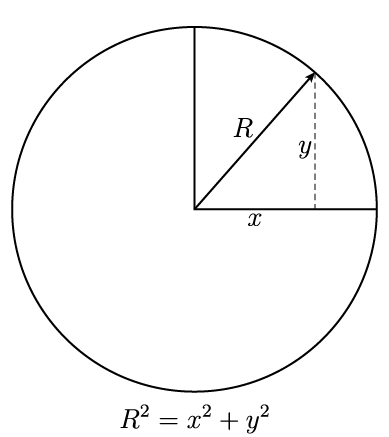
איור 2. אם כדור הארץ חג סביב השמש, רדיוס מסלולו R נשאר בעינו. הקואורדינטות של כדור הארץ, x ו-y, משתנות ברציפות עם התנועה, אבל R הוא אינווריאנטי. לפי משפט פיתגורס, ידוע לנו כי x2 + y2 = R2. לכן משוואת ניוטון סימטרית כשהיא מבוטאת גם במונחי R (מפני ש-R הוא אינווריאנטי) וגם במונחי x ו-y (באמצעות משפט פיתגורס).
1. סטיבן הוקינג, "האם קרב קץ הפיזיקה התיאורטית?", בתוך חורים שחורים, גורי יקומים ומסות אחרות; תר' ע' לוטם (אור יהודה: ספריית מעריב, 1994): 53-71.
2. בעבר, רבים מענקי הפיזיקה ניסו ליצור תיאוריית שדה מאוחדת משלהם, והדבר לא עלה בידי איש מהם. במבט לאחור, נוכל לראות שתיאוריית שדה מאוחדת חייבת לענות על שלוש דרישות:
1.עליה לכלול את כל תורת היחסות הכללית של איינשטיין.
2.עליה לכלול את המודל הסטנדרטי של החלקיקים התת־אטומיים.
3.עליה לספק תוצאות סופיות מבחינה מתמטית.
ארווין שרֵדִינגֶר, אחד מאבותיה של תורת הקוונטים, העלה הצעה לתיאוריית שדה מאוחדת שלמען האמת, איינשטיין חקר אותה לפניו. היא נכשלה מפני שהיא לא הצטמצמה כהלכה לתורת היחסות הכללית ולא יכלה להסביר את משוואות מקסוול. (כמו כן, לא היה בה שום תיאור של אלקטרונים או של אטומים.)
גם וולפגנג פָּאוּלִי וּורנר הַייזֶנבֶּרג הציעו תיאוריית שדה מאוחדת. היא כללה את שדות החומר הפֶרמיוני, אבל לא היה אפשר לבצע בה רה־נורמליזציה, והיא לא כללה את המודל הקווארקי, שהיה עתיד להופיע עשרות שנים אחריה.
איינשטיין עצמו חקר שורה של תיאוריות, שנכשלו כולן בסופו של דבר. בלשון טכנית, הוא ניסה להכליל את טֶנסור המֶטריקה של הכבידה ואת סמלי כּרִיסטוֹפֶל באופן שיכלול טנסורים אנטי־סימטריים, בניסיון לכלול את תיאוריית מקסוול ואת התיאוריה שלו. הוא העלה חרס בידו. לא היה די בהגדלת מספר השדות בתיאוריה המקורית של איינשטיין כדי להסביר את משוואות מקסוול. גישה זו גם לא הזכירה כלל את החומר.
במרוצת השנים נעשו כמה ניסיונות להוסיף בפשטות שדות חומר למשוואות איינשטיין, אבל הוּכח שהם כשלו ברמה הקוונטית החד־לולאתית. בפועל, נעשה שימוש במחשבים לחישוב פיזור הגרוויטונים ברמה הקוונטית החד־לולאתית, והוכח באופן מסקני שהוא אינסופי. עד כה, הדרך הידועה היחידה לסילוק האינסופים הללו ברמה החד־לולאתית הנמוכה ביותר היא הכללת על־סימטריה.
רעיון קיצוני יותר הציע כבר ב-1919 תאודור קָלוּצָה, שביטא את משוואות איינשטיין בחמישה ממדים. מה שמרשים הוא שכאשר מכרבלים ממד אחד למעגל זערורי, מוצאים את משוואות מקסוול צמודות לשדה הכבידה של איינשטיין. ואמנם, איינשטיין חקר את הגישה הזאת אבל נטש אותה בסופו של דבר, מפני שאיש לא הבין כיצד אפשר להקריס ממד אחד. מאוחר יותר שולבה גישה זו בתורת המיתרים, המקריסה עשרה ממדים לארבעה ממדים, ותוך כדי כך מחוללת שדה יָאנג־מִילס. כיוון שכך, מבין הגישות המרובות שננקטו בחתירה לתיאוריית שדה מאוחדת, היחידה שנותרה כיום היא גישת קלוצה הגְבה־ממדית, כשהיא מוכללת כך שתקיף על־סימטריה, על־מיתרים ועל־קרומיות.
בזמן האחרון הופיעה תיאוריה בשם כבידה קוונטית לולאתית. היא חוקרת את התיאוריה הארבע־ממדית המקורית של איינשטיין בדרך חדשה. אבל זוהי תיאוריה של כבידה בלבד, בלי שום אלקטרונים או חלקיקים תת־אטומיים, ומשום כך אינה יכולה להיחשב כתיאוריית שדה מאוחדת. היא אינה מזכירה כלל את המודל הסטנדרטי, מפני שאין בה שדות חומר. זאת ועוד, לא ברור אם הפיזור הרב־לולאתי בפורמליזם הזה הוא אכן סופי. לפי אחד הניחושים, התנגשות של שתי לולאות תספק תוצאות מתבדרות.
3. Steven Weinberg, Dreams of a Final Theory (New York: Pantheon, 1992), 11




אין עדיין תגובות